선형 회귀는 하나 이상의 특성과 연속적인 타깃 변수 사이의 관계를 모델링하는 것이 목적이다.
지도 학습의 분류 알고리즘과 달리, 회귀는 범주형 클래스 레이블이 아니라 연속적인 출력값을 예측한다.
따라서 산업 현장 애플리케이션은 물론 과학 문제를 해결하기 위한 매력적인 도구이다.
단순 선형 회귀(Simple Linear Regression)
하나의 특성(설명 변수(explanatory variable) x)과 연속적인 타깃(응답 변수(response variable) y) 사이의 관계를 모델링한다.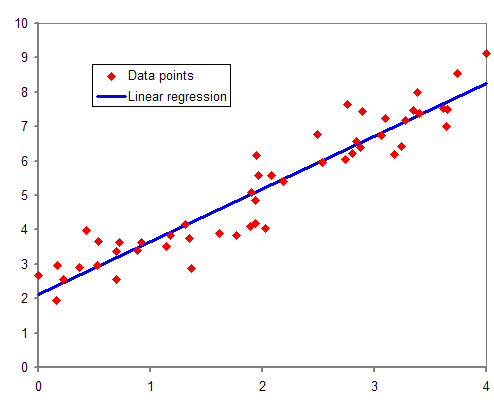
특성과 타깃 사이의 관계를 설명해 주는 선형 방정식의 가중치를 학습하는 것이 목적이다.
데이터에 가장 잘 맞는 위의 직선을 회귀 직선(Regression Line)이라고 한다.
회귀 직선과 훈련 샘플 사이의 직선 거리를 오프셋(offset) 또는 예측 오차인 잔차(residual)라고 한다.
다중 선형 회귀(Multiple Linear Regression)
특성이 하나인 특별한 경우를 단순 선형 회귀라고 하며, 여러 개의 특성이 있는 경우 이를 다중 선형 회귀라고 한다.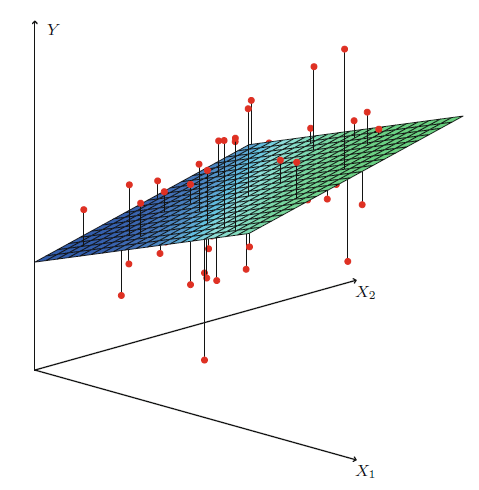
특성이 2개인 다중 선형 회귀
특성이 2개인 다중 선형 회귀정적인 이미지로 그려진 다변량 회귀의 초평면은 3차원 산점도만 되어도 이해하기 어렵다.